ABU ALI HASAN IBN AL-HAITHAM (ALHAZEN) (965 - 1040 AD) Al-Haitham, known in the West as Alhazen, is considered as the father of modern optics.
Alhazen
From Wikipedia, the free encyclopedia
Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham (
Arabic:
أبو علي، الحسن بن الحسن بن الهيثم), frequently referred to as
Ibn al-Haytham (Arabic:
ابن الهيثم,
Latinized as
Alhazen[Notes 1] or
Alhacen;
c. 965 –
c. 1040), was an
Arab,
[8] Muslim,
polymath and
philosopher who made significant contributions to the principles of
optics,
astronomy,
mathematics,
meteorology,
[9] visual perception and the
scientific method.
In
medieval Europe, he was honored as
Ptolemaeus Secundus ("
Ptolemy the Second")
[10] or simply called "The Physicist".
[11] He is also sometimes called
al-Basri (Arabic:
البصري) after
Basra, his birthplace.
[12] He spent most of his life close to the court of the
Fatimid Caliphate in
Cairo and earned his living authoring various treatises and tutoring members of the nobilities.
[13]
Overview
Biography
Born c. 965 in
Basra, which was then part of the
Buyid emirate,
[1] to an
Arab family.
[14][15]
He arrived in Cairo under the reign of
Fatimid Caliph
al-Hakim, a patron of the sciences who was particularly interested in astronomy.
[16] Ibn al-Haytham has proposed to the Caliph a
hydraulic project to improve regulation of the
flooding of the Nile, a task requiring an early attempt at building a
dam at the present site of the
Aswan Dam.
[16] His field work convinced him of the technical impracticality of this scheme.
[17] Al-Haytham continued to live in Cairo, in the neighborhood of the famous
University of al-Azhar, until his death after 1040.
[10] Legend has it that after deciding the scheme was impractical and fearing the
caliph's anger, Alhazen
feigned madness and was kept under
house arrest from 1011 until al-Hakim's death in 1021.
[18] During this time, he wrote his influential
Book of Optics and continued to write further treatises on astronomy, geometry, number theory, optics and natural philosophy.
Among his students were
Sorkhab (
Sohrab), a
Persian from
Semnan who was his student for over 3 years, and
Abu al-Wafa Mubashir ibn Fatek, an
Egyptian prince who learned mathematics from Alhazen.
[19]
Legacy
Front page of the Opticae Thesaurus, which included the first printed Latin translation of Alhazen's Book of Optics.
The illustration incorporates many examples of optical phenomena
including perspective effects, the rainbow, mirrors, and refraction.
Alhazen made significant contributions to optics, number theory,
geometry, astronomy and natural philosophy. Alhazen's work on optics is
credited with contributing a new emphasis on experiment.
His main work,
Kitab al-Manazir (
Book of Optics) was known in Islamicate societies mainly, but not exclusively, through the thirteenth-century commentary by
Kamāl al-Dīn al-Fārisī, the
Tanqīḥ al-Manāẓir
li-dhawī l-abṣār wa l-baṣā'ir.
[20] In
al-Andalus, it was used by the eleventh-century prince of the Banu Hud dynasty of Zaragossa and author of an important mathematical text,
al-Mu'taman ibn Hūd. A Latin translation of the
Kitab al-Manazir was made probably in the late twelfth or early thirteenth century.
[21][22] This translation was read by and greatly influenced a number of scholars in Catholic Europe including:
Roger Bacon,
[23] Robert Grosseteste,
[24] Witelo,
Giambattista della Porta,
[25] Leonardo Da Vinci,
[26] Galileo Galilei,
[27] Christian Huygens,
[28] René Descartes,
[27] and
Johannes Kepler.
[29] His research in
catoptrics (the study of optical systems using mirrors) centred on spherical and
parabolic mirrors and
spherical aberration. He made the observation that the ratio between the
angle of incidence and
refraction does not remain constant, and investigated the
magnifying power of a
lens. His work on catoptrics also contains the problem known as "
Alhazen's problem".
[30] Meanwhile in the Islamic world, Alhazen's work influenced
Averroes' writings on optics,
[31] and his legacy was further advanced through the 'reforming' of his
Optics by Persian scientist
Kamal al-Din al-Farisi (died ca. 1320) in the latter's
Kitab Tanqih al-Manazir (
The Revision of [Ibn al-Haytham's]
Optics).
[32]
Alhazen wrote as many as 200 books, although only 55 have survived.
Some of his treatises on optics survived only through Latin translation.
During the Middle Ages his books on
cosmology were translated into Latin,
Hebrew and other languages. The crater
Alhazen on the Moon is named in his honour,
[33] as was the
asteroid 59239 Alhazen.
[34]
In honour of Alhazen, the Aga Khan University (Pakistan) named its
Ophthalmology endowed chair as "The Ibn-e-Haitham Associate Professor
and Chief of Ophthalmology".
[35] Alhazen, by the name Ibn al-Haytham, is featured on the obverse of the Iraqi 10,000-
dinar banknote issued in 2003,
[36] and on 10-dinar notes from 1982. A research facility that
UN weapons inspectors suspected of conducting chemical and biological weapons research in
Saddam Hussein's Iraq was also named after him.
[36][37]
One of the major scientific anniversaries that will be celebrated during the 2015
International Year of Light is: the works on optics by Ibn Al-Haytham (1015).
Book of Optics
Main article:
Book of Optics
Alhazen's most famous work
[38] is his seven-volume treatise on
optics Kitab al-Manazir (
Book of Optics), written from 1011 to 1021.
Optics was
translated into Latin by an unknown scholar at the end of the 12th century or the beginning of the 13th century.
[39] It was printed by
Friedrich Risner in 1572, with the title
Opticae thesaurus: Alhazeni Arabis libri septem, nuncprimum editi; Eiusdem liber De Crepusculis et nubium ascensionibus
(English : Optics treasure: Arab Alhazeni seven books, published for
the first time: The book of the Twilight of the clouds and ascensions).
[40]
Risner is also the author of the name variant "Alhazen"; before Risner
he was known in the west as Alhacen, which is the correct transcription
of the Arabic name.
[41] This work enjoyed a great reputation during the
Middle Ages. Works by Alhazen on geometric subjects were discovered in the
Bibliothèque nationale in
Paris
in 1834 by E. A. Sedillot. In all, A. Mark Smith has accounted for 18
full or near-complete manuscripts, and five fragments, which are
preserved in 14 locations, including one in the
Bodleian Library at
Oxford, and one in the library of
Bruges.
[42]
Theory of vision
Alhazen on Iraqi 10 dinars
Two major theories on vision prevailed in
classical antiquity. The first theory, the
emission theory, was supported by such thinkers as
Euclid and
Ptolemy, who believed that sight worked by the eye emitting
rays of
light. The second theory, the intromission theory supported by
Aristotle and his followers, had physical forms entering the eye from an object. Previous Islamic writers (such as
al-Kindi) had argued essentially on Euclidean, Galenist, or Aristotelian lines. The strongest influence on the
Book of Optics was from Ptolemy's
Optics, while the description of the anatomy and physiology of the eye was based on Galen's account.
[43]
Alhazen's achievement was to come up with a theory which successfully
combined parts of the mathematical ray arguments of Euclid, the medical
tradition of
Galen,
and the intromission theories of Aristotle. Alhazen's intromission
theory followed al-Kindi (and broke with Aristotle) in asserting that
"from each point of every colored body, illuminated by any light, issue
light and color along every straight line that can be drawn from that
point".
[44]
This however left him with the problem of explaining how a coherent
image was formed from many independent sources of radiation; in
particular, every point of an object would send rays to every point on
the eye. What Alhazen needed was for each point on an object to
correspond to one point only on the eye.
[44]
He attempted to resolve this by asserting that only perpendicular rays
from the object would be perceived by the eye; for any one point on the
eye, only the ray which reached it directly, without being refracted by
any other part of the eye, would be perceived. He argued using a
physical analogy that perpendicular rays were stronger than oblique
rays; in the same way that a ball thrown directly at a board might break
the board, whereas a ball thrown obliquely at the board would glance
off, perpendicular rays were stronger than refracted rays, and it was
only perpendicular rays which were perceived by the eye. As there was
only one perpendicular ray that would enter the eye at any one point,
and all these rays would converge on the centre of the eye in a cone,
this allowed him to resolve the problem of each point on an object
sending many rays to the eye; if only the perpendicular ray mattered,
then he had a one-to-one correspondence and the confusion could be
resolved.
[45] He later asserted (in book seven of the
Optics) that other rays would be refracted through the eye and perceived
as if perpendicular.
[46]
His arguments regarding perpendicular rays do not clearly explain why
only perpendicular rays were perceived; why would the weaker oblique rays not be perceived more weakly?
[47] His later argument that refracted rays would be perceived as if perpendicular does not seem persuasive.
[48]
However, despite its weaknesses, no other theory of the time was so
comprehensive, and it was enormously influential, particularly in
Western Europe: "Directly or indirectly, his
De Aspectibus inspired much of the activity in optics which occurred between the 13th and 17th centuries."
[49] Kepler's later theory of the
retinal
image (which resolved the problem of the correspondence of points on an
object and points in the eye) built directly on the conceptual
framework of Alhazen.
[49]
Alhazen showed through experiment that light travels in straight lines, and carried out various experiments with
lenses,
mirrors,
refraction, and
reflection.
[30]
He was the first to consider separately the vertical and horizontal
components of reflected and refracted light rays, which was an important
step in understanding optics geometrically.
[50]
The
camera obscura was known to the
ancient Chinese and was described by the
Han Chinese polymathic genius Shen Kuo in his scientific book
Dream Pool Essays which was printed and published in the year 1088 C.E.. Aristotle had discussed the basic principle behind it in his
Problems, however Alhazen's work also contained the first clear description, outside of
China, of
camera obscura in the areas of the
middle east,
Europe,
Africa and
India.
[51] and early analysis
[52] of the device.
Alhazen studied the process of sight, the structure of the eye, image formation in the eye, and the
visual system. Ian P. Howard argued in a 1996
Perception
article that Alhazen should be credited with many discoveries and
theories which were previously attributed to Western Europeans writing
centuries later. For example, he described what became in the 19th
century
Hering's law of equal innervation; he had a description of vertical
horopters which predates
Aguilonius by 600 years and is actually closer to the modern definition than Aguilonius's; and his work on
binocular disparity was repeated by Panum in 1858.
[53]
Craig Aaen-Stockdale, while agreeing that Alhazen should be credited
with many advances, has expressed some caution, especially when
considering Alhazen in isolation from
Ptolemy,
who Alhazen was extremely familiar with. Alhazen corrected a
significant error of Ptolemy regarding binocular vision, but otherwise
his account is very similar; Ptolemy also attempted to explain what is
now called Hering's law.
[54] In general, Alhazen built on and expanded the optics of Ptolemy.
[55][56] In a more detailed account of Ibn al-Haytham's contribution to the study of binocular vision based on Lejeune
[57] and Sabra,
[58] Raynaud
[59]
showed that the concepts of correspondence, homonymous and crossed
diplopia were in place in Ibn al-Haytham's optics. But contrary to
Howard, he explained why Ibn al-Haytham did not give the circular figure
of the horopter and why, by reasoning experimentally, he was in fact
closer to the discovery of Panum's fusional area than that of the
Vieth-Müller circle. In this regard, Ibn al-Haytham's theory of
binocular vision faced two main limits: the lack of recognition of the
role of the retina, and obviously the lack of an experimental
investigation of ocular tracts.
Alhazen's most original contribution was that after describing how he
thought the eye was anatomically constructed, he went on to consider
how this anatomy would behave functionally as an optical system.
[60]
His understanding of pinhole projection from his experiments appears to
have influenced his consideration of image inversion in the eye,
[61] which he sought to avoid.
[62]
He maintained that the rays that fell perpendicularly on the lens (or
glacial humor as he called it) were further refracted outward as they
left the glacial humor and the resulting image thus passed upright into
the optic nerve at the back of the eye.
[63] He followed
Galen in believing that the
lens was the receptive organ of sight, although some of his work hints that he thought the
retina was also involved.
[64]
Alhazen's synthesis of light and vision adhered to the Aristotelian
scheme, exhaustively describing the process of vision in a logical,
complete fashion.
[65]
Scientific method
| “ |
The duty of the man who investigates the
writings of scientists, if learning the truth is his goal, is to make
himself an enemy of all that he reads, and,.. attack it from every side.
He should also suspect himself as he performs his critical examination
of it, so that he may avoid falling into either prejudice or leniency. |
” |
|
|
An aspect associated with Alhazen's optical research is related to systemic and methodological reliance on experimentation (
i'tibar)(Arabic: إعتبار) and
controlled testing in his scientific inquiries. Moreover, his experimental directives rested on combining classical physics (
ilm tabi'i) with mathematics (
ta'alim; geometry in particular). This mathematical-physical approach to experimental science supported most of his propositions in
Kitab al-Manazir (
The Optics;
De aspectibus or
Perspectivae) and grounded his theories of vision, light and colour, as well as his research in catoptrics and
dioptrics (the study of the refraction of light).
[32] According to Matthias Schramm, Alhazen:
was the first to make a systematic use of the method of varying the
experimental conditions in a constant and uniform manner, in an
experiment showing that the intensity of the light-spot formed by the
projection of the moonlight through two small apertures onto a screen diminishes constantly as one of the apertures is gradually blocked up.[66]
G. J. Toomer expressed some skepticism regarding Schramm's view,
arguing that caution is needed to avoid reading anachronistically
particular passages in Alhazen's very large body of work, and while
acknowledging Alhazen's importance in developing experimental
techniques, argued that he should not be considered in isolation from
other Islamic and ancient thinkers.
[67]
A. Mark Smith's critical editions (2001, 2006, 2008, 2010) of
De Aspectibus
contain a Latin glossary with page numbers of each occurrence of the
words, to illustrate Alhacen's experimental viewpoint. Smith shows that
Alhacen was received well in the West because he reinforced the
importance of the Hellenic tradition to them.
[68]
Alhazen's problem
His work on
catoptrics in Book V of the Book of Optics contains a discussion of what is now known as Alhazen's problem, first formulated by
Ptolemy in 150 AD. It comprises drawing lines from two points in the
plane of a circle meeting at a point on the
circumference and making equal angles with the
normal at that point. This is equivalent to finding the point on the edge of a circular
billiard table
at which a cue ball at a given point must be aimed in order to carom
off the edge of the table and hit another ball at a second given point.
Thus, its main application in optics is to solve the problem, "Given a
light source and a spherical mirror, find the point on the mirror where
the light will be reflected to the eye of an observer." This leads to an
equation of the fourth degree.
[12][69] This eventually led Alhazen to derive a formula for the sum of
fourth powers,
where previously only the formulas for the sums of squares and cubes
had been stated. His method can be readily generalized to find the
formula for the sum of any integral powers, although he did not himself
do this (perhaps because he only needed the fourth power to calculate
the volume of the paraboloid he was interested in). He used his result
on sums of integral powers to perform what would now be called an
integration, where the formulas for the sums of integral squares and fourth powers allowed him to calculate the volume of a
paraboloid.
[70] Alhazen eventually solved the problem using
conic sections
and a geometric proof. His solution was extremely long and complicated
and may not have been understood by mathematicians reading him in Latin
translation. Later mathematicians used
Descartes' analytical methods to analyse the problem,
[71] with a new solution being found in 1997 by the Oxford mathematician
Peter M. Neumann.
[72] Recently,
Mitsubishi Electric Research Laboratories
(MERL) researchers Amit Agrawal, Yuichi Taguchi and Srikumar Ramalingam
solved the extension of Alhazen's problem to general rotationally
symmetric quadric mirrors including hyperbolic, parabolic and elliptical
mirrors.
[73]
They showed that the mirror reflection point can be computed by solving
an eighth degree equation in the most general case. If the camera (eye)
is placed on the axis of the mirror, the degree of the equation reduces
to six.
[74]
Alhazen's problem can also be extended to multiple refractions from a
spherical ball. Given a light source and a spherical ball of certain
refractive index, the closest point on the spherical ball where the
light is refracted to the eye of the observer can be obtained by solving
a tenth degree equation.
[74]
Refraction
Smith 2010 has noted that Alhazen's treatment of refraction describes an experimental setup without publication of data.
[75] Ptolemy published his experimental results for refraction, in contrast. One generation before Alhazen,
Ibn Sahl
discovered his statement of the lengths of the hypotenuse for each
incident and refracted right triangle, respectively. This is equivalent
to Descartes' formulation for refraction. Alhazen's convention for
describing the incident and refracted angles is still in use. His
failure to publish his data is an open question.
Other contributions
The Kitab al-Manazir (Book of Optics) describes several experimental
observations that Alhazen made and how he used his results to explain
certain optical phenomena using mechanical analogies. He conducted
experiments with
projectiles, and a description of his conclusions is: "it was only the impact of
perpendicular projectiles on surfaces which was forceful enough to enable them to penetrate whereas the
oblique
ones were deflected. For example, to explain refraction from a rare to a
dense medium, he used the mechanical analogy of an iron ball thrown at a
thin slate covering a wide hole in a metal sheet. A perpendicular throw
would break the slate and pass through, whereas an oblique one with
equal force and from an equal distance would not."
[76]
He also used this result to explain how intense, direct light hurts the
eye, using a mechanical analogy: "Alhazen associated 'strong' lights
with perpendicular rays and 'weak' lights with oblique ones. The obvious
answer to the problem of multiple rays and the eye was in the choice of
the perpendicular ray since there could only be one such ray from each
point on the surface of the object which could penetrate the eye."
[76]
Sudanese psychologist Omar Khaleefa has argued that Alhazen should be considered be the "founder of
experimental psychology", for his pioneering work on the psychology of visual perception and
optical illusions.
[77] Khaleefa has also argued that Alhazen should also be considered the "founder of
psychophysics", a sub-discipline and precursor to modern psychology.
[77]
Although Alhazen made many subjective reports regarding vision, there
is no evidence that he used quantitative psychophysical techniques and
the claim has been rebuffed.
[54]
Alhazen offered an explanation of the
Moon illusion, an illusion that played an important role in the scientific tradition of medieval Europe.
[78]
Many authors repeated explanations that attempted to solve the problem
of the Moon appearing larger near the horizon than it does when higher
up in the sky, a debate that is still unresolved. Alhazen argued against
Ptolemy's refraction theory, and defined the problem in terms of
perceived, rather than real, enlargement. He said that judging the
distance of an object depends on there being an uninterrupted sequence
of intervening bodies between the object and the observer. When the Moon
is high in the sky there are no intervening objects, so the Moon
appears close. The perceived size of an object of constant angular size
varies with its perceived distance. Therefore, the Moon appears closer
and smaller high in the sky, and further and larger on the horizon.
Through works by
Roger Bacon,
John Pecham
and Witelo based on Alhazen's explanation, the Moon illusion gradually
came to be accepted as a psychological phenomenon, with the refraction
theory being rejected in the 17th century.
[79] Although Alhazen is often credited with the perceived distance explanation, he was not the first author to offer it.
Cleomedes (
c. 2nd century) gave this account (in addition to refraction), and he credited it to
Posidonius (
c. 135-50 BC).
[80] Ptolemy may also have offered this explanation in his
Optics, but the text is obscure.
[81]
Alhazen's writings were more widely available in the Middle Ages than
those of these earlier authors, and that probably explains why Alhazen
received the credit.
Other works on physics
Optical treatises
Besides the
Book of Optics, Alhazen wrote several other treatises on the same subject, including his
Risala fi l-Daw’ (
Treatise on Light). He investigated the properties of
luminance, the
rainbow,
eclipses, twilight, and
moonlight. Experiments with mirrors and
magnifying lenses provided the foundation for his theories on
catoptrics.
[82]
Celestial physics
Alhazen discussed the
physics of the celestial region in his
Epitome of Astronomy,
arguing that Ptolemaic models needed to be understood in terms of
physical objects rather than abstract hypotheses; in other words that it
should be possible to create physical models where (for example) none
of the celestial bodies would collide with each other. The suggestion of
mechanical models for the Earth centred
Ptolemaic model
"greatly contributed to the eventual triumph of the Ptolemaic system
among the Christians of the West". Alhazen's determination to root
astronomy in the realm of physical objects was important however,
because it meant astronomical hypotheses "were accountable to the
laws of physics", and could be criticised and improved upon in those terms.
[83]
He also wrote
Maqala fi daw al-qamar (
On the Light of the Moon).
Mechanics
In his work, Alhazen discussed theories on the
motion of a body.
[82] In his
Treatise on Place, Alhazen disagreed with
Aristotle's view that nature abhors a void, and he used
geometry in an attempt to demonstrate that place (
al-makan) is the imagined three-dimensional void between the inner surfaces of a containing body.
[84]
Astronomical works
On the Configuration of the World
In his
On the Configuration of the World Alhazen presented a detailed description of the physical structure of the earth:
The earth as a whole is a round sphere whose center is the center of
the world. It is stationary in its [the world's] middle, fixed in it and
not moving in any direction nor moving with any of the varieties of
motion, but always at rest.[85]
The book is a non-technical explanation of Ptolemy's
Almagest, which was eventually translated into
Hebrew and
Latin in the 13th and 14th centuries and subsequently had an influence on astronomers such as
Georg von Peuerbach[1] during the European
Middle Ages and
Renaissance.
[86][87]
Doubts Concerning Ptolemy
In his
Al-Shukūk ‛alā Batlamyūs, variously translated as
Doubts Concerning Ptolemy or
Aporias against Ptolemy, published at some time between 1025 and 1028, Alhazen criticized
Ptolemy's
Almagest,
Planetary Hypotheses, and
Optics, pointing out various contradictions he found in these works, particularly in astronomy. Ptolemy's
Almagest concerned mathematical theories regarding the motion of the planets, whereas the
Hypotheses
concerned what Ptolemy thought was the actual configuration of the
planets. Ptolemy himself acknowledged that his theories and
configurations did not always agree with each other, arguing that this
was not a problem provided it did not result in noticeable error, but
Alhazen was particularly scathing in his criticism of the inherent
contradictions in Ptolemy's works.
[88] He considered that some of the mathematical devices Ptolemy introduced into astronomy, especially the
equant,
failed to satisfy the physical requirement of uniform circular motion,
and noted the absurdity of relating actual physical motions to imaginary
mathematical points, lines and circles:
[89]
Ptolemy assumed an arrangement (hay'a) that cannot exist, and
the fact that this arrangement produces in his imagination the motions
that belong to the planets does not free him from the error he committed
in his assumed arrangement, for the existing motions of the planets
cannot be the result of an arrangement that is impossible to exist...
[F]or a man to imagine a circle in the heavens, and to imagine the
planet moving in it does not bring about the planet's motion.[90][91]
Having pointed out the problems, Alhazen appears to have intended to
resolve the contradictions he pointed out in Ptolemy in a later work.
Alhazen's belief was that there was a "true configuration" of the
planets which Ptolemy had failed to grasp; his intention was to complete
and repair Ptolemy's system, not to replace it completely.
[88]
In the
Doubts Concerning Ptolemy Alhazen set out his views on
the difficulty of attaining scientific knowledge and the need to
question existing authorities and theories:
Truth is sought for itself [but] the truths, [he warns] are immersed
in uncertainties [and the scientific authorities (such as Ptolemy, whom
he greatly respected) are] not immune from error...[58]
He held that the criticism of existing theories—which dominated this
book—holds a special place in the growth of scientific knowledge.
Model of the Motions of Each of the Seven Planets
Alhazen's
The Model of the Motions of Each of the Seven Planets was written
c.
1038. Only one damaged manuscript has been found, with only the
introduction and the first section, on the theory of planetary motion,
surviving. (There was also a second section on astronomical calculation,
and a third section, on astronomical instruments.) Following on from
his
Doubts on Ptolemy, Alhazen described a new, geometry-based
planetary model, describing the motions of the planets in terms of
spherical geometry, infinitesimal geometry and trigonometry. He kept a
geocentric universe and assumed that celestial motions are uniformly
circular, which required the inclusion of
epicycles to explain observed motion, but he managed to eliminate Ptolemy's
equant.
In general, his model made no attempt to provide a causal explanation
of the motions, but concentrated on providing a complete, geometric
description which could be used to explain observed motions, without the
contradictions inherent in Ptolemy's model.
[92]
Other astronomical works
Alhazen wrote a total of twenty-five astronomical works, some concerning technical issues such as
Exact Determination of the Meridian,
a second group concerning accurate astronomical observation, a third
group concerning various astronomical problems and questions such as the
location of the
Milky Way; Alhazen argued for a distant location, based on the fact that it does not move in relation to the fixed stars.
[93] The fourth group consists of ten works on astronomical theory, including the
Doubts and
Model of the Motions discussed above.
[94]
Mathematical works
In
mathematics, Alhazen built on the mathematical works of
Euclid and
Thabit ibn Qurra and worked on "the beginnings of the link between
algebra and
geometry."
[95]
He developed a formula for adding the first 100 natural numbers, using a geometric proof to prove the formula.
[96]
Geometry
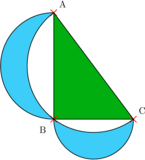
The lunes of Alhazen. The two blue lunes together have the same area as the green right triangle.
Alhazen explored what is now known as the
Euclidean parallel postulate, the fifth
postulate in
Euclid's Elements, using a
proof by contradiction,
[97] and in effect introducing the concept of motion into geometry.
[98] He formulated the
Lambert quadrilateral, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral".
[99] His theorems on
quadrilaterals, including the Lambert quadrilateral, were the first theorems on
elliptical geometry and
hyperbolic geometry. These theorems, along with his alternative postulates, such as Playfair's axiom, can be seen as marking the beginning of
non-Euclidean geometry. His work had a considerable influence on its development among the later Persian geometers
Omar Khayyám and
Nasīr al-Dīn al-Tūsī, and the European geometers
Witelo,
Gersonides, and
Alfonso.
[100]
In elementary geometry, Alhazen attempted to solve the problem of
squaring the circle using the area of
lunes (crescent shapes), but later gave up on the impossible task.
[12] The two lunes formed from a
right triangle
by erecting a semicircle on each of the triangle's sides, inward for
the hypotenuse and outward for the other two sides, are known as the
lunes of Alhazen; they have the same total area as the triangle itself.
[101]
Number theory
His contributions to
number theory include his work on
perfect numbers. In his
Analysis and Synthesis, Alhazen may have been the first to state that every even perfect number is of the form 2
n−1(2
n − 1) where 2
n − 1 is
prime, but he was not able to prove this result successfully (
Euler later proved it in the 18th century).
[12]
Alhazen solved problems involving
congruences using what is now called
Wilson's theorem. In his
Opuscula,
Alhazen considers the solution of a system of congruences, and gives
two general methods of solution. His first method, the canonical method,
involved Wilson's theorem, while his second method involved a version
of the
Chinese remainder theorem.
[12]
Other works
Influence of Melodies on the Souls of Animals
Alhazen also wrote a
Treatise on the Influence of Melodies on the Souls of Animals,
although no copies have survived. It appears to have been concerned
with the question of whether animals could react to music, for example
whether a camel would increase or decrease its pace.
Engineering
In
engineering, one account of his career as a
civil engineer has him summoned to Egypt by the Fatimid
Caliph,
Al-Hakim bi-Amr Allah, to regulate the
flooding of the
Nile River. He carried out a detailed scientific study of the annual
inundation of the Nile River, and he drew plans for building a
dam, at the site of the modern-day
Aswan Dam. His field work, however, later made him aware of the impracticality of this scheme, and he soon
feigned madness so he could avoid punishment from the Caliph.
[102]
Philosophy
In his
Treatise on Place, Alhazen disagreed with
Aristotle's view that nature abhors a
void, and he used
geometry in an attempt to demonstrate that place (
al-makan) is the imagined three-dimensional void between the inner surfaces of a containing body.
[84] Abd-el-latif, a supporter of Aristotle's philosophical view of place, later criticized the work in
Fi al-Radd ‘ala Ibn al-Haytham fi al-makan (
A refutation of Ibn al-Haytham’s place) for its geometrization of place.
[84]
Alhazen also discussed
space perception and its
epistemological implications in his
Book of Optics.
In "tying the visual perception of space to prior bodily experience,
Alhacen unequivocally rejected the intuitiveness of spatial perception
and, therefore, the autonomy of vision. Without tangible notions of
distance and size for correlation, sight can tell us next to nothing
about such things."
[103]
Theology
Alhazen was a devout
Muslim, though it is uncertain which branch of
Islam he followed. He may have been either a follower of the
Ash'ari school of
Sunni Islamic theology according to
Ziauddin Sardar[104] and Lawrence Bettany
[105] (and opposed to the views of the
Mu'tazili school),
[105] a follower of the Mu'tazili school of Islamic theology according to Peter Edward Hodgson,
[106] or a possibly follower of
Shia Islam according to
A. I. Sabra.
[107]
Alhazen wrote a work on Islamic theology in which he discussed
prophethood and developed a system of philosophical criteria to discern its false claimants in his time.
[108] He also wrote a treatise entitled
Finding the Direction of Qibla by Calculation in which he discussed finding the
Qibla, where
Salat prayers are directed towards, mathematically.
[109]
He wrote in his
Doubts Concerning Ptolemy:
Truth is sought for its own sake ... Finding the truth is difficult,
and the road to it is rough. For the truths are plunged in obscurity.
... God, however, has not preserved the scientist from error and has not
safeguarded science from shortcomings and faults. If this had been the
case, scientists would not have disagreed upon any point of science...[110]
In
The Winding Motion, Alhazen further wrote:
From the statements made by the noble Shaykh,
it is clear that he believes in Ptolemy's words in everything he says,
without relying on a demonstration or calling on a proof, but by pure
imitation (taqlid); that is how experts in the prophetic
tradition have faith in Prophets, may the blessing of God be upon them.
But it is not the way that mathematicians have faith in specialists in
the demonstrative sciences.[111]
Alhazen described his theology:
I constantly sought knowledge and truth, and it became my belief that for gaining access to the effulgence and closeness to God, there is no better way than that of searching for truth and knowledge.[112]
List of works
According to medieval biographers, Alhazen wrote more than 200 works
on a wide range of subjects, of which at least 96 of his scientific
works are known. Most of his works are now lost, but more than 50 of
them have survived to some extent. Nearly half of his surviving works
are on mathematics, 23 of them are on astronomy, and 14 of them are on
optics, with a few on other subjects.
[113] Not all his surviving works have yet been studied, but some of the ones that have are given below.
[94][109]
- Book of Optics (كتاب المناظر )
- Analysis and Synthesis (مقالة في التحليل والتركيب)
- Balance of Wisdom (ميزان الحكمة. )
- Corrections to the Almagest (تصويبات على المجسطي. )
- Discourse on Place (مقالة في المكان. )
- Exact Determination of the Pole (التحديد الدقيق للقطب)
- Exact Determination of the Meridian (رسالة في الشفق)
- Finding the Direction of Qibla by Calculation (كيفية حساب اتجاه القبلة)
- Horizontal Sundials (المزولة الأفقية)
- Hour Lines
- Doubts Concerning Ptolemy (شكوك على بطليموس.)
- Maqala fi'l-Qarastun (مقالة في قرسطون)
- On Completion of the Conics (إكمال المخاريط )
- On Seeing the Stars (رؤية الكواكب )
- On Squaring the Circle (مقالة فی تربیع الدائرة )
- On the Burning Sphere ( المرايا المحرقة بالدوائر)
- On the Configuration of the World (تكوين العالم.-)
- On the Form of Eclipse (مقالة فی صورة الکسوف-)
- On the Light of Stars (مقالة في ضوء النجوم - )
- On the Light of the Moon (مقالة في ضوء القمر)
- On the Milky Way (مقالة في درب التبانة.)
- On the Nature of Shadows (كيفيات الإظلال)
- On the Rainbow and Halo (مقالة في قوس قزح)
- Opuscula
- Resolution of Doubts Concerning the Almagest
- Resolution of Doubts Concerning the Winding Motion
- The Correction of the Operations in Astronomy
- The Different Heights of the Planets
- The Direction of Mecca (اتجاه القبلة)
- The Model of the Motions of Each of the Seven Planets (نماذج حركات الكواكب السبعة)
- The Model of the Universe (نموذج الكون)
- The Motion of the Moon (حركة القمر)
- The Ratios of Hourly Arcs to their Heights
- The Winding Motion (الحركة المتعرجة)
- Treatise on Light (رسالة في الضوء)
- Treatise on Place (رسالة في المكان)
- Treatise on the Influence of Melodies on the Souls of Animals (تأثير اللحون الموسيقية في النفوس الحيوانية )
- (كتاب في تحليل المسائل الهندسية )
- (الجامع في أصول الحساب)
- قول فی مساحة الکرة.
- القول المعروف بالغریب فی حساب المعاملات)
- خواص المثلث من جهة العمود.)
- رسالة فی مساحة المسجم المکافی
- شرح أصول إقليدس
- المرايا المحرقة بالقطوع
Lost works
- A Book in which I have Summarized the Science of Optics from the
Two Books of Euclid and Ptolemy, to which I have added the Notions of
the First Discourse which is Missing from Ptolemy's Book[114]
Commemorations
Ibn Al-Haytham's work has been commemorated by the naming of the
Alhazen crater on the
moon after him. The asteroid
59239 Alhazen was also named in his honour.
In 2014, the "
Hiding in the Light" episode of
Cosmos: A Spacetime Odyssey, presented by
Neil deGrasse Tyson, focused on the accomplishments of Ibn al-Haytham. He was voiced by
Alfred Molina in the episode.
UNESCO has declared 2015 the
International Year of Light.
Amongst others, this will be celebrating Ibn Al-Haytham's achievements
in optics, mathematics and astronomy. An international campaign, created
by the
1001 Inventions organisation, titled
1001 Inventions and the World of Ibn Al-Haytham
featuring a series of interactive exhibits, workshops and live shows
about his work will partner with science centers, science festivals,
museums, and educational institutions, as well as digital and social
media platforms.
[115] 1001 Inventions is a founding partner of the
International Year of Light.
[116]
UNESCO's website
[117] on Ibn al-Haytham copies a part from
Jim Al-Khalili's popular history
Pathfinders: The Golden Age of Arabic Science.
See also
Notes
References
Alhazen (Ibn al-Haytham)
Alhazen made significant contributions to optics, number theory, geometry, astronomy and natural philosophy. Alhazen's work on optics is credited with contributing a new emphasis on experiment.Front page of the Opticae Thesaurus, which included the first printed Latin translation of Alhazen's Book of Optics. The illustration incorporates many examples of optical phenomena including perspective effects, the rainbow, mirrors, and refraction.
Two major theories on vision prevailed in classical antiquity. The first theory, the emission theory, was supported by such thinkers as Euclid and Ptolemy, who believed that sight worked by the eye emitting rays of light. The second theory, the intromission theory supported by Aristotle and his followers, had physical forms entering the eye from an object. Previous Islamic writers (such as al-Kindi) had argued essentially on Euclidean, Galenist, or Aristotelian lines. The strongest influence on the Book of Optics was from Ptolemy's Optics, while the description of the anatomy and physiology of the eye was based on Galen's account.[43] Alhazen's achievement was to come up with a theory which successfully combined parts of the mathematical ray arguments of Euclid, the medical tradition of Galen, and the intromission theories of Aristotle. Alhazen's intromission theory followed al-Kindi (and broke with Aristotle) in asserting that "from each point of every colored body, illuminated by any light, issue light and color along every straight line that can be drawn from that point".[44] This however left him with the problem of explaining how a coherent image was formed from many independent sources of radiation; in particular, every point of an object would send rays to every point on the eye. What Alhazen needed was for each point on an object to correspond to one point only on the eye.[44] He attempted to resolve this by asserting that only perpendicular rays from the object would be perceived by the eye; for any one point on the eye, only the ray which reached it directly, without being refracted by any other part of the eye, would be perceived. He argued using a physical analogy that perpendicular rays were stronger than oblique rays; in the same way that a ball thrown directly at a board might break the board, whereas a ball thrown obliquely at the board would glance off, perpendicular rays were stronger than refracted rays, and it was only perpendicular rays which were perceived by the eye. As there was only one perpendicular ray that would enter the eye at any one point, and all these rays would converge on the centre of the eye in a cone, this allowed him to resolve the problem of each point on an object sending many rays to the eye; if only the perpendicular ray mattered, then he had a one-to-one correspondence and the confusion could be resolved.[45] He later asserted (in book seven of the Optics) that other rays would be refracted through the eye and perceived as if perpendicular.[46]Alhazen on Iraqi 10 dinars
Hevelius's Selenographia, showing Alhasen [sic] representing reason, and Galileo representing the senses.
Alhazen explored what is now known as the Euclidean parallel postulate, the fifth postulate in Euclid's Elements, using a proof by contradiction,[97] and in effect introducing the concept of motion into geometry.[98] He formulated the Lambert quadrilateral, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral".[99] His theorems on quadrilaterals, including the Lambert quadrilateral, were the first theorems on elliptical geometry and hyperbolic geometry. These theorems, along with his alternative postulates, such as Playfair's axiom, can be seen as marking the beginning of non-Euclidean geometry. His work had a considerable influence on its development among the later Persian geometers Omar Khayyám and Nasīr al-Dīn al-Tūsī, and the European geometers Witelo, Gersonides, and Alfonso.[100]The lunes of Alhazen. The two blue lunes together have the same area as the green right triangle.
Thank you for nice information. Please visit our web :
ReplyDeleteDais Isnafirlah
Dais Isnafirlah