begin quote from:

In planetary sciences, the moment of inertia factor or normalized polar moment of inertia is a dimensionless quantity that characterizes the radial distribution of mass inside a planet or satellite. Since a moment of inertia must have dimensions of mass times length squared, the moment of inertia factor is the coefficient that multiplies these.

Definition[edit]

For a planetary body with principal moments of inertia $A<B<C$ , the moment of inertia factor is defined as

{\frac {C}{MR^{2}}}

,

where C is the polar moment of inertia of the body, M is the mass of the body, and R is the mean radius of the body.^[1]^[2] For a sphere with uniform density, $C/MR^{2}=0.4$ .^{[note 1]}^{[note 2]} For a differentiated planet or satellite, where there is an increase of density with depth, $C/MR^{2}<0.4$ . The quantity is a useful indicator of the presence and extent of a planetary core, because a greater departure from the uniform-density value of 0.4 conveys a greater degree of concentration of dense materials towards the center.

Solar System values[edit]

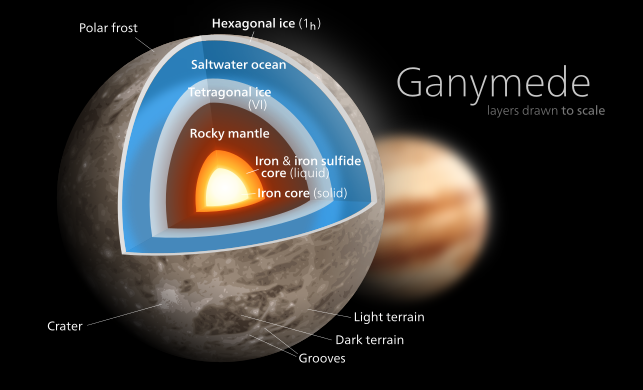
The Sun has by far the lowest moment of inertia factor value among Solar System bodies; it has by far the highest central density (162 g/cm³,^[3]^{[note 3]} compared to ~13 for Earth^[4]^[5]) and a relatively low average density (1.41 g/cm³ versus 5.5 for Earth). Saturn has the lowest value among the gas giants in part because it has the lowest bulk density (0.687 g/cm³).^[6] Ganymede has the lowest moment of inertia factor among solid bodies in the Solar System because of its fully differentiated interior,^[7]^[8] a result in part of tidal heating due to the Laplace resonance,^[9] as well as its substantial component of low density water ice. Callisto is similar in size and bulk composition to Ganymede, but is not part of the orbital resonance and is less differentiated.^[7]^[8] The Moon is thought to have a small core, but its interior is otherwise relatively homogenous.^[10]^[11]

Body	Value	Source	Notes
Sun	0.070	^[3]	Not measured
Mercury	0.346 ± 0.014	^[12]
Venus	0.337 ± 0.024	^[13]
Earth	0.3307	^[14]
Moon	0.3929 ± 0.0009	^[15]
Mars	0.3644 ± 0.0005	^[16]
Ceres	0.36 ± 0.15^{[note 4]}	^[18]	Not measured (range reflects different assumptions for original spin rate^[18])
Jupiter	0.2756 ± 0.0006	^[19]	Not measured (two-layer model calculations constrained by Juno gravity data^[19])
Io	0.37824 ± 0.00022	^[20]	Not measured (Darwin-Radau relation)
Europa	0.346 ± 0.005	^[20]	Not measured (Darwin-Radau relation)
Ganymede	0.3115 ± 0.0028	^[20]	Not measured (Darwin-Radau relation)
Callisto	0.3549 ± 0.0042	^[20]	Not measured (Darwin-Radau relation)
Saturn	0.22	^[21]	Not measured (Darwin-Radau relation)
Enceladus	0.3305 ± 0.0025	^[22]	Not measured (Darwin-Radau relation)
Rhea	0.3911 ± 0.0045	^[23]	Not measured (Darwin-Radau relation)
Titan	0.341	^[24]	Not measured (Darwin-Radau relation)
Uranus	0.23	^[25]	Not measured (approximate solution to Clairaut's equation)
Neptune	0.23	^[25]	Not measured (approximate solution to Clairaut's equation)

Measurement[edit]

The polar moment of inertia is traditionally determined by combining measurements of spin quantities (spin precession rate and/or obliquity) with gravity quantities (coefficients of a spherical harmonic representation of the gravity field). These geodetic data usually require an orbiting spacecraft to collect.

Approximation[edit]

For bodies in hydrostatic equilibrium, the Darwin–Radau relation can provide estimates of the moment of inertia factor on the basis of shape, spin, and gravity quantities.^[26]

Role in interior models[edit]

The moment of inertia factor provides an important constraint for models representing the interior structure of a planet or satellite. At a minimum, acceptable models of the density profile must match the volumetric mass density and moment of inertia factor of the body.

Gallery of internal structure models[edit]

The Sun (C/MR² = 0.070)
Saturn (C/MR² = 0.22)
Ganymede (C/MR² = 0.3115)
Earth (C/MR² = 0.3307)
Callisto (C/MR² = 0.3549)
The Moon (C/MR² = 0.3929)

Notes[edit]

^ For a sphere with uniform density we can calculate the moment of inertia and the mass by integrating over disks from the "south pole" to the "north pole". Using a density of 1, a disk of radius $r$ has a moment of inertia of
$\int _{0}^{r}2\pi r^{3}\ dr={\frac {\pi r^{4}}{2}}$
whereas the mass is
$\int _{0}^{r}2\pi r\ dr=\pi r^{2}$
Letting $r=R\cos \theta$ and integrating over $R\sin \theta$ we get:
${\begin{aligned}{\frac {C}{R^{5}}}&={\frac {\pi }{2}}\int _{-1}^{1}\cos ^{4}\theta \ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-\sin ^{2}\theta )^{2}\ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-2\sin ^{2}\theta +\sin ^{4}\theta )d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(d\sin \theta -{\frac {2}{3}}d\sin ^{3}\theta +{\frac {1}{5}}d\sin ^{5}\theta )\\&={\frac {8}{15}}\pi \end{aligned}}$
${\begin{aligned}{\frac {M}{R^{3}}}&=\pi \int _{-1}^{1}\cos ^{2}\theta \ d\sin \theta \\&=\pi \int _{-1}^{1}(1-\sin ^{2}\theta )d\sin \theta \\&=\pi \int _{-1}^{1}(d\sin \theta -{\frac {1}{3}}d\sin ^{3}\theta )\\&={\frac {4}{3}}\pi \end{aligned}}$
This gives $C/MR^{2}=0.4$ .
^ For several other examples (in which the rotation axis is the axis of symmetry if not otherwise specified), a solid cone has a factor of 0.3; a uniform thin rod (rotating about its center perpendicularly to its axis, so R is length/2) has a factor of 1/3; a hollow cone or a solid cylinder has a factor of 0.5; a hollow sphere has factor of 2/3; a hollow open-ended cylinder has a factor of 1.0.
^ A star's central density tends to increase over the course of its lifetime, aside from during brief core nuclear fusion ignition events like the helium flash.
^ The value given for Ceres is the mean moment of inertia, which is thought to better represent its interior structure than the polar moment of inertia, due to its high polar flattening.^[17]

[3] For a sphere with uniform density we can calculate the moment of inertia and the mass by integrating over disks from the "south pole" to the "north pole". Using a density of 1, a disk of radius $r$ has a moment of inertia of
$\int _{0}^{r}2\pi r^{3}\ dr={\frac {\pi r^{4}}{2}}$
whereas the mass is
$\int _{0}^{r}2\pi r\ dr=\pi r^{2}$
Letting $r=R\cos \theta$ and integrating over $R\sin \theta$ we get:
${\begin{aligned}{\frac {C}{R^{5}}}&={\frac {\pi }{2}}\int _{-1}^{1}\cos ^{4}\theta \ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-\sin ^{2}\theta )^{2}\ d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(1-2\sin ^{2}\theta +\sin ^{4}\theta )d\sin \theta \\&={\frac {\pi }{2}}\int _{-1}^{1}(d\sin \theta -{\frac {2}{3}}d\sin ^{3}\theta +{\frac {1}{5}}d\sin ^{5}\theta )\\&={\frac {8}{15}}\pi \end{aligned}}$
${\begin{aligned}{\frac {M}{R^{3}}}&=\pi \int _{-1}^{1}\cos ^{2}\theta \ d\sin \theta \\&=\pi \int _{-1}^{1}(1-\sin ^{2}\theta )d\sin \theta \\&=\pi \int _{-1}^{1}(d\sin \theta -{\frac {1}{3}}d\sin ^{3}\theta )\\&={\frac {4}{3}}\pi \end{aligned}}$
This gives $C/MR^{2}=0.4$ .

[4] For several other examples (in which the rotation axis is the axis of symmetry if not otherwise specified), a solid cone has a factor of 0.3; a uniform thin rod (rotating about its center perpendicularly to its axis, so R is length/2) has a factor of 1/3; a hollow cone or a solid cylinder has a factor of 0.5; a hollow sphere has factor of 2/3; a hollow open-ended cylinder has a factor of 1.0.

[6] A star's central density tends to increase over the course of its lifetime, aside from during brief core nuclear fusion ignition events like the helium flash.

[21] The value given for Ceres is the mean moment of inertia, which is thought to better represent its interior structure than the polar moment of inertia, due to its high polar flattening.^[17]

[1]

[2]

[note 1]

[note 2]

[3]

[note 3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[note 4]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[17]

Intuitive fred888

Tuesday, May 31, 2022

Ganymede has the lowest moment of inertia factor of any solid body in the Solar System and is the only moon known to have a magnetic field.

begin quote from:

Moment of inertia factor

Contents