begin quote from:
Byzantine fault
A Byzantine fault (also interactive consistency, source congruency, error avalanche, Byzantine agreement problem, Byzantine generals problem, and Byzantine failure[1]) is a condition of a computer system, particularly distributed computing systems, where components may fail and there is imperfect information on whether a component has failed. The term takes its name from an allegory, the "Byzantine Generals Problem",[2] developed to describe a situation in which, in order to avoid catastrophic failure of the system, the system's actors must agree on a concerted strategy, but some of these actors are unreliable.
In a Byzantine fault, a component such as a server can inconsistently appear both failed and functioning to failure-detection systems, presenting different symptoms to different observers. It is difficult for the other components to declare it failed and shut it out of the network, because they need to first reach a consensus regarding which component has failed in the first place.
Byzantine fault tolerance (BFT) is the dependability of a fault-tolerant computer system to such conditions.
Characteristics[edit]
A Byzantine fault is any fault presenting different symptoms to different observers.[3] A Byzantine failure is the loss of a system service due to a Byzantine fault in systems that require consensus.[4]
The objective of Byzantine fault tolerance is to be able to defend against failures of system components with or without symptoms that prevent other components of the system from reaching an agreement among themselves, where such an agreement is needed for the correct operation of the system.
The remaining operationally correct components of a Byzantine fault tolerant system will be able to continue providing the system's service as originally intended, assuming there are a sufficient number of accurately-operating components to maintain the service.
Byzantine failures are considered the most general and most difficult class of failures among the failure modes. The so-called fail-stop failure mode occupies the simplest end of the spectrum. Whereas fail-stop failure mode simply means that the only way to fail is a node crash, detected by other nodes, Byzantine failures imply no restrictions, which means that the failed node can generate arbitrary data, including data that makes it appear like a functioning node. Thus, Byzantine failures can confuse failure detection systems, which makes fault tolerance difficult. Despite the analogy, a Byzantine failure is not necessarily a security problem involving hostile human interference: it can arise purely from electrical or software faults.
The terms fault and failure are used here according to the standard definitions[5] originally created by a joint committee on "Fundamental Concepts and Terminology" formed by the IEEE Computer Society's Technical Committee on Dependable Computing and Fault-Tolerance and IFIP Working Group 10.4 on Dependable Computing and Fault Tolerance.[6] A version of these definitions is also described in the Dependability Wikipedia page.
Caveat[edit]
Byzantine fault tolerance is only concerned with broadcast correctness, that is, the property that when one component broadcasts a single consistent value to other components (i.e., sends the same value to the other components), they all receive exactly the same value, or in the case that the broadcaster is not consistent, the other components agree on a common value. This kind of fault tolerance does not encompass the correctness of the value itself; for example, an adversarial component that deliberately sends an incorrect value, but sends that same value consistently to all components, will not be caught in the Byzantine fault tolerance scheme.
Formal definition[edit]
Setting:[7] Given a system of n components, t of which are dishonest, and assuming only point-to-point channel between all the components.
Whenever a component A tries to broadcast a value x, the other components are allowed to discuss with each other and verify the consistency of A's broadcast, and eventually settle on a common value y.
Property: The system is said to resist Byzantine faults if a component A can broadcast a value x, and then:
- If A is honest, then all honest components agree on the value x.
- In any case, all honest components agree on the same value y.
Variants: The problem has been studied in the case of both synchronous and asynchronous communications.
The communication graph above is assumed to be the complete graph (i.e. each component can discuss with every other), but the communication graph can be restricted.
It can also be relaxed in a more "realistic" problem where the faulty components do not collude together in an attempt to lure the others into error. It is in this setting that practical algorithms have been devised.
History[edit]
The problem of obtaining Byzantine consensus was conceived and formalized by Robert Shostak, who dubbed it the interactive consistency problem. This work was done in 1978 in the context of the NASA-sponsored SIFT[8] project in the Computer Science Lab at SRI International. SIFT (for Software Implemented Fault Tolerance) was the brain child of John Wensley, and was based on the idea of using multiple general-purpose computers that would communicate through pairwise messaging in order to reach a consensus, even if some of the computers were faulty.
At the beginning of the project, it was not clear how many computers in total are needed to guarantee that a conspiracy of n faulty computers could not "thwart" the efforts of the correctly-operating ones to reach consensus. Shostak showed that a minimum of 3n+1 are needed, and devised a two-round 3n+1 messaging protocol that would work for n=1. His colleague Marshall Pease generalized the algorithm for any n > 0, proving that 3n+1 is both necessary and sufficient. These results, together with a later proof by Leslie Lamport of the sufficiency of 3n using digital signatures, were published in the seminal paper, Reaching Agreement in the Presence of Faults.[9] The authors were awarded the 2005 Edsger W. Dijkstra Prize for this paper.
To make the interactive consistency problem easier to understand, Lamport devised a colorful allegory in which a group of army generals formulate a plan for attacking a city. In its original version, the story cast the generals as commanders of the Albanian army. The name was changed, eventually settling on "Byzantine", at the suggestion of Jack Goldberg to future-proof any potential offense giving.[10] This formulation of the problem, together with some additional results, were presented by the same authors in their 1982 paper, "The Byzantine Generals Problem".[11]
Analogy[edit]
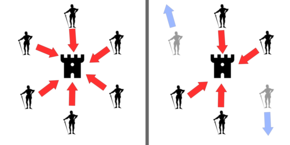
In its simplest form, a number of generals are attacking a fortress and must decide as a group only whether to attack or retreat. Some generals may prefer to attack, while others prefer to retreat. The important thing is that all generals agree on a common decision, for a halfhearted attack by a few generals would become a rout, and would be worse than either a coordinated attack or a coordinated retreat.
The problem is complicated by the presence of treacherous generals who may not only cast a vote for a suboptimal strategy, they may do so selectively. For instance, if nine generals are voting, four of whom support attacking while four others are in favor of retreat, the ninth general may send a vote of retreat to those generals in favor of retreat, and a vote of attack to the rest. Those who received a retreat vote from the ninth general will retreat, while the rest will attack (which may not go well for the attackers). The problem is complicated further by the generals being physically separated and having to send their votes via messengers who may fail to deliver votes or may forge false votes.
Resolution[edit]
Byzantine fault tolerance can be achieved if the loyal (non-faulty) generals have a majority agreement on their strategy. There can be a default vote value given to missing messages. For example, missing messages can be given a "null" value. Further, if the agreement is that the null votes are in the majority, a pre-assigned default strategy can be used (e.g. retreat).[11]
The typical mapping of this story onto computer systems is that the computers are the generals and their digital communication system links are the messengers. Although the problem is formulated in the analogy as a decision-making and security problem, in electronics, it cannot be solved simply by cryptographic digital signatures, because failures such as incorrect voltages can propagate through the encryption process. Thus, a component may appear functioning to one component and faulty to another, which prevents forming a consensus as to whether the component is faulty or not.
Examples[edit]
Several examples of Byzantine failures that have occurred are given in two equivalent journal papers.[3][4] These and other examples are described on the NASA DASHlink web pages.[12] These web pages also describe some phenomena that can cause Byzantine faults.
Byzantine errors were observed infrequently and at irregular points during endurance testing for the newly constructed Virginia class submarines, at least through 2005 (when the issues were publicly reported).[13]
Early solutions[edit]
Several solutions were described by Lamport, Shostak, and Pease in 1982.[11] They began by noting that the Generals' Problem can be reduced to solving a "Commander and Lieutenants" problem where loyal Lieutenants must all act in unison and that their action must correspond to what the Commander ordered in the case that the Commander is loyal:
- One solution considers scenarios in which messages may be forged, but which will be Byzantine-fault-tolerant as long as the number of disloyal generals is less than one third of the generals. The impossibility of dealing with one-third or more traitors ultimately reduces to proving that the one Commander and two Lieutenants problem cannot be solved, if the Commander is traitorous. To see this, suppose we have a traitorous Commander A, and two Lieutenants, B and C: when A tells B to attack and C to retreat, and B and C send messages to each other, forwarding A's message, neither B nor C can figure out who is the traitor, since it is not necessarily A—another Lieutenant could have forged the message purportedly from A. It can be shown that if n is the number of generals in total, and t is the number of traitors in that n, then there are solutions to the problem only when n > 3t and the communication is synchronous (bounded delay).[14]
- A second solution requires unforgeable message signatures. For security-critical systems, digital signatures (in modern computer systems, this may be achieved in practice using public-key cryptography) can provide Byzantine fault tolerance in the presence of an arbitrary number of traitorous generals. However, for safety-critical systems (where "security" addresses intelligent threats while "safety" addresses the inherent dangers of an activity or mission), simple error detecting codes, such as CRCs, provide weaker but often sufficient coverage at a much lower cost. This is true for both Byzantine and non-Byzantine faults. Furthermore, sometimes security measures weaken safety and vice versa. Thus, cryptographic digital signature methods are not a good choice for safety-critical systems, unless there is also a specific security threat as well.[15] While error detecting codes, such as CRCs, are better than cryptographic techniques, neither provide adequate coverage for active electronics in safety-critical systems. This is illustrated by the Schrödinger CRC scenario where a CRC-protected message with a single Byzantine faulty bit presents different data to different observers and each observer sees a valid CRC.[3][4]
- Also presented is a variation on the first two solutions allowing Byzantine-fault-tolerant behavior in some situations where not all generals can communicate directly with each other.
Several system architectures were designed c. 1980 that implemented Byzantine fault tolerance. These include: Draper's FTMP,[16] Honeywell's MMFCS,[17] and SRI's SIFT.[8]
Advanced solutions[edit]
In 1999, Miguel Castro and Barbara Liskov introduced the "Practical Byzantine Fault Tolerance" (PBFT) algorithm,[18] which provides high-performance Byzantine state machine replication, processing thousands of requests per second with sub-millisecond increases in latency.
After PBFT, several BFT protocols were introduced to improve its robustness and performance. For instance, Q/U,[19] HQ,[20] Zyzzyva,[21] and ABsTRACTs,[22] addressed the performance and cost issues; whereas other protocols, like Aardvark[23] and RBFT,[24] addressed its robustness issues. Furthermore, Adapt[25] tried to make use of existing BFT protocols, through switching between them in an adaptive way, to improve system robustness and performance as the underlying conditions change. Furthermore, BFT protocols were introduced that leverage trusted components to reduce the number of replicas, e.g., A2M-PBFT-EA[26] and MinBFT.[27]
Motivated by PBFT, Tendermint BFT[28] was introduced for partial asynchronous networks and it is mainly used for Proof of Stake blockchains.
BFT implementations[edit]
One example of BFT in use is bitcoin, a peer-to-peer digital cash system.[29] The bitcoin network works in parallel to generate a blockchain with proof-of-work allowing the system to overcome Byzantine failures and reach a coherent global view of the system's state.
Some aircraft systems, such as the Boeing 777 Aircraft Information Management System (via its ARINC 659 SAFEbus network),[30][31] the Boeing 777 flight control system,[32] and the Boeing 787 flight control systems use Byzantine fault tolerance; because these are real-time systems, their Byzantine fault tolerance solutions must have very low latency. For example, SAFEbus can achieve Byzantine fault tolerance within the order of a microsecond of added latency.
Some spacecraft flight systems such as that of the SpaceX Dragon[33] consider Byzantine fault tolerance in their design.
Byzantine fault tolerance mechanisms use components that repeat an incoming message (or just its signature) to other recipients of that incoming message. All these mechanisms make the assumption that the act of repeating a message blocks the propagation of Byzantine symptoms. For systems that have a high degree of safety or security criticality, these assumptions must be proven to be true to an acceptable level of fault coverage. When providing proof through testing, one difficulty is creating a sufficiently wide range of signals with Byzantine symptoms.[34] Such testing likely will require specialized fault injectors.[35][36]
Software[edit]
- UpRight is an open source library for constructing services that tolerate both crashes ("up") and Byzantine behaviors ("right") that incorporates many of these protocols' innovations.[37]
- The BFT-SMaRt library is a high-performance Byzantine fault-tolerant state machine replication library developed in Java. This library implements a protocol very similar to PBFT's, plus complementary protocols which offer state transfer and on-the-fly reconfiguration of hosts. BFT-SMaRt is the most recent effort to implement state machine replication, still being actively maintained.[38]
- Archistar utilizes a slim BFT layer for communication. It prototypes a secure multi-cloud storage system using Java licensed under LGPLv2. Focus lies on simplicity and readability, it aims to be the foundation for further research projects.[39][40]
- Askemos is a concurrent, garbage-collected, persistent programming platform atop of replicated state machines which tolerates Byzantine faults. It prototypes an execution environment facilitating smart contracts.[41]
No comments:
Post a Comment