end quote from:
Difference Between TCP and IP | Difference Between
www.differencebetween.net/.../difference-between</...Difference Between TCP and HTTP; Difference Between IPSEC and GRE; Difference Between VPN and MPLS; ... "Difference Between TCP and IP." DifferenceBetween.net.- end quote:When he or she is talking about the bottom of the network stack of protocols not actually having protocols it is because this is machine language which is all numbers sent in bytes of information in zeros and 1s or better said in on switches and off switches which is what machine language is composed of. It doesn't need protocols because all machine language is basically the same in any language. It is only when people need to read what is going on that you move up into a language that functions higher on the stack than machine language.Machine language is all in binary which is a way to convert zeros and 1s to our base 10 numeric system we use every day and then binary is also used to covert to a alpha numeric system so both numbers and letters can be sent thousands of miles without protocol.Though it is possible though clumsy and time consuming to write in binary machine language it is easier for humans to write in computer languages like HTML especially working on web pages. But, then protocols are needed when communicating in HTML or other compatible languages worldwide. This is when you need TCP/IP and HTTP for the protocols.begin quote from:
Binary number - Wikipedia
en.wikipedia.org/wiki/Binary_numeral_systemIn mathematics and digital electronics, a binary number is a number expressed in the binary numeral system or base-2 numeral system which represents numeric values ...Binary | Definition of Binary by Merriam-Webster
www.merriam-webster.com/dictionary/binaryDefine binary: something made of two things or parts specifically : binary star — binary in a sentenceFree Binary Code Translator | Translate Binary Code to Text
www.binarytranslator.comConvert binary codes, text to binary, decimal to octal, binary to hexadecimal, decimal to binary, and much more with binary converter online for free.Binary number
From Wikipedia, the free encyclopedia(Redirected from Binary numeral system)Numeral systems 
Hindu–Arabic numeral system East Asian Alphabetic Former Positional systems by base Non-standard positional numeral systems List of numeral systems Dear readers in the U.S., today we ask you to help Wikipedia. To protect our independence, we'll never run ads. We're sustained by donations averaging about $15. Only a tiny portion of our readers give. If everyone reading this right now gave $3, we could keep Wikipedia thriving for years to come. That's right, the price of a cup of coffee is all we need. If Wikipedia is useful to you, please take one minute to keep it online and growing. Thank you.
In mathematics and digital electronics, a binary number is a number expressed in the binary numeral system or base-2 numeral system which represents numeric values using two different symbols: typically 0 (zero) and 1 (one). The base-2 system is a positional notation with a radix of 2. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by almost all modern computers and computer-based devices. Each digit is referred to as a bit.Close
Contents
History
The modern binary number system was devised by Gottfried Leibniz in 1679 and appears in his article Explication de l'Arithmétique Binaire (published in 1703). Systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. Leibniz was specifically inspired by the Chinese I Ching.
Egypt
See also: Ancient Egyptian mathematicsThe scribes of ancient Egypt used two different systems for their fractions, Egyptian fractions (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye of Horus, although this has been disputed). Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt, approximately 1200 BC.[1]Arithmetic values represented by parts of the Eye of Horus
The method used for ancient Egyptian multiplication is also closely related to binary numbers. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it; the order in which these steps are to be performed is given by the binary representation of the second number. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus, which dates to around 1650 BC.[2]
China
The I Ching dates from the 9th century BC in China.[3] The binary notation in the I Ching is used to interpret its quaternary divination technique.[4]Daoist Bagua
It is based on taoistic duality of yin and yang.[5] eight trigrams (Bagua) and a set of 64 hexagrams ("sixty-four" gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou Dynasty of ancient China.[3]
The Song Dynasty scholar Shao Yong (1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically.[4] Viewing the least significant bit on top of single hexagrams in Shao Yong's square and reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63. [6]
India
The Indian scholar Pingala (c. 2nd century BC) developed a binary system for describing prosody.[7][8] He used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code.[9][10] Pingala's Hindu classic titled Chandaḥśāstra (8.23) describes the formation of a matrix in order to give a unique value to each meter. The binary representations in Pingala's system increases towards the right, and not to the left like in the binary numbers of the modern, Western positional notation.[11][12]
Other cultures
The residents of the island of Mangareva in French Polynesia were using a hybrid binary-decimal system before 1450.[13] Slit drums with binary tones are used to encode messages across Africa and Asia.[5] Sets of binary combinations similar to the I Ching have also been used in traditional African divination systems such as Ifá as well as in medieval Western geomancy. The base-2 system utilized in geomancy had long been widely applied in sub-Saharan Africa.
Western predecessors to Leibniz
In 1605 Francis Bacon discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text.[14] Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: "provided those objects be capable of a twofold difference only; as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature".[14] (See Bacon's cipher.)
Leibniz and the I Ching
The full title of Leibniz's article is translated into English as the "Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi".[15] (1703). Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows:[15]Gottfried Leibniz
- 0 0 0 1 numerical value 20
- 0 0 1 0 numerical value 21
- 0 1 0 0 numerical value 22
- 1 0 0 0 numerical value 23
[A concept that] is not easy to impart to the pagans, is the creation ex nihilo through God's almighty power. Now one can say that nothing in the world can better present and demonstrate this power than the origin of numbers, as it is presented here through the simple and unadorned presentation of One and Zero or Nothing.
— Leibniz's letter to the Duke of Brunswick attached with the I Ching hexagrams[16]Later developments
In 1854, British mathematician George Boole published a landmark paper detailing an algebraic system of logic that would become known as Boolean algebra. His logical calculus was to become instrumental in the design of digital electronic circuitry.[19]George Boole
In 1937, Claude Shannon produced his master's thesis at MIT that implemented Boolean algebra and binary arithmetic using electronic relays and switches for the first time in history. Entitled A Symbolic Analysis of Relay and Switching Circuits, Shannon's thesis essentially founded practical digital circuit design.[20]
In November 1937, George Stibitz, then working at Bell Labs, completed a relay-based computer he dubbed the "Model K" (for "Kitchen", where he had assembled it), which calculated using binary addition.[21] Bell Labs authorized a full research program in late 1938 with Stibitz at the helm. Their Complex Number Computer, completed 8 January 1940, was able to calculate complex numbers. In a demonstration to the American Mathematical Society conference at Dartmouth College on 11 September 1940, Stibitz was able to send the Complex Number Calculator remote commands over telephone lines by a teletype. It was the first computing machine ever used remotely over a phone line. Some participants of the conference who witnessed the demonstration were John von Neumann, John Mauchly and Norbert Wiener, who wrote about it in his memoirs.[22][23][24]
The Z1 computer, which was designed and built by Konrad Zuse between 1935 and 1938, used Boolean logic and binary floating point numbers.[25]
Representation
Any number can be represented by any sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667:
1 0 1 0 0 1 1 0 1 1 | ― | ― ― | | ― | | ☒ ☐ ☒ ☐ ☐ ☒ ☒ ☐ ☒ ☒ y n y n n y y n y y The numeric value represented in each case is dependent upon the value assigned to each symbol. In a computer, the numeric values may be represented by two different voltages; on a magnetic disk, magnetic polarities may be used. A "positive", "yes", or "on" state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.A binary clock might use LEDs to express binary values. In this clock, each column of LEDs shows a binary-coded decimal numeral of the traditional sexagesimal time.
In keeping with customary representation of numerals using Arabic numerals, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed or suffixed in order to indicate their base, or radix. The following notations are equivalent:
- 100101 binary (explicit statement of format)
- 100101b (a suffix indicating binary format; also known as Intel convention[26][27])
- 100101B (a suffix indicating binary format)
- bin 100101 (a prefix indicating binary format)
- 1001012 (a subscript indicating base-2 (binary) notation)
- %100101 (a prefix indicating binary format; also known as Motorola convention[26][27])
- 0b100101 (a prefix indicating binary format, common in programming languages)
- 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
Counting in binary
Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiar decimal counting system as a frame of reference.Decimal
patternBinary
number0 0 1 1 2 10 3 11 4 100 5 101 6 110 7 111 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111
Decimal counting
Decimal counting uses the ten symbols 0 through 9. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the first digit. When the available symbols for this position are exhausted, the least significant digit is reset to 0, and the next digit of higher significance (one position to the left) is incremented (overflow), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows:
- 000, 001, 002, ... 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented)
- 010, 011, 012, ...
- ...
- 090, 091, 092, ... 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented)
- 100, 101, 102, ...
Binary counting
Binary counting follows the same procedure, except that only the two symbols 0 and 1 are available. Thus, after a digit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next digit to the left:This counter shows how to count in binary from numbers zero through thirty-one.
- 0000,
- 0001, (rightmost digit starts over, and next digit is incremented)
- 0010, 0011, (rightmost two digits start over, and next digit is incremented)
- 0100, 0101, 0110, 0111, (rightmost three digits start over, and the next digit is incremented)
- 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
- 1001012 = [ ( 1 ) × 25 ] + [ ( 0 ) × 24 ] + [ ( 0 ) × 23 ] + [ ( 1 ) × 22 ] + [ ( 0 ) × 21 ] + [ ( 1 ) × 20 ]
- 1001012 = [ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]
- 1001012 = 3710
Fractions
Fractions in binary only terminate if the denominator has 2 as the only prime factor. As a result, 1/10 does not have a finite binary representation, and this causes 10 × 0.1 not to be precisely equal to 1 in floating point arithmetic. As an example, to interpret the binary expression for 1/3 = .010101..., this means: 1/3 = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + ... = 0.3125 + ... An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.
Fraction Decimal Binary Fractional approximation 1/1 1 or 0.999... 1 or 0.111... 1/2 + 1/4 + 1/8... 1/2 0.5 or 0.4999... 0.1 or 0.0111... 1/4 + 1/8 + 1/16 . . . 1/3 0.333... 0.010101... 1/4 + 1/16 + 1/64 . . . 1/4 0.25 or 0.24999... 0.01 or 0.00111... 1/8 + 1/16 + 1/32 . . . 1/5 0.2 or 0.1999... 0.00110011... 1/8 + 1/16 + 1/128 . . . 1/6 0.1666... 0.0010101... 1/8 + 1/32 + 1/128 . . . 1/7 0.142857142857... 0.001001... 1/8 + 1/64 + 1/512 . . . 1/8 0.125 or 0.124999... 0.001 or 0.000111... 1/16 + 1/32 + 1/64 . . . 1/9 0.111... 0.000111000111... 1/16 + 1/32 + 1/64 . . . 1/10 0.1 or 0.0999... 0.000110011... 1/16 + 1/32 + 1/256 . . . 1/11 0.090909... 0.00010111010001011101... 1/16 + 1/64 + 1/128 . . . 1/12 0.08333... 0.00010101... 1/16 + 1/64 + 1/256 . . . 1/13 0.076923076923... 0.000100111011000100111011... 1/16 + 1/128 + 1/256 . . . 1/14 0.0714285714285... 0.0001001001... 1/16 + 1/128 + 1/1024 . . . 1/15 0.0666... 0.00010001... 1/16 + 1/256 . . . 1/16 0.0625 or 0.0624999... 0.0001 or 0.0000111... 1/32 + 1/64 + 1/128 . . . Binary arithmetic
Arithmetic in binary is much like arithmetic in other numeral systems. Addition, subtraction, multiplication, and division can be performed on binary numerals.
Addition
Main article: binary adderThe simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying:The circuit diagram for a binary half adder, which adds two bits together, producing sum and carry bits.
- 0 + 0 → 0
- 0 + 1 → 1
- 1 + 0 → 1
- 1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 21) )
- 5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 101) )
- 7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 101) )
1 1 1 1 1 (carried digits) 0 1 1 0 1 + 1 0 1 1 1 ------------- = 1 0 0 1 0 0 = 36In this example, two numerals are being added together: 011012 (1310) and 101112 (2310). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 102. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 102 again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 112. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 1001002 (36 decimal).
When computers must add two numbers, the rule that: x xor y = (x + y) mod 2 for any two bits x and y allows for very fast calculation, as well.
Long carry method
A simplification for many binary addition problems is the Long Carry Method or Brookhouse Method of Binary Addition. This method is generally useful in any binary addition where one of the numbers contains a long "string" of ones. It is based on the simple premise that under the binary system, when given a "string" of digits composed entirely of n ones (where: n is any integer length), adding 1 will result in the number 1 followed by a string of n zeros. That concept follows, logically, just as in the decimal system, where adding 1 to a string of n 9s will result in the number 1 followed by a string of n 0s:
Binary Decimal 1 1 1 1 1 likewise 9 9 9 9 9 + 1 + 1 ——————————— ——————————— 1 0 0 0 0 0 1 0 0 0 0 0Such long strings are quite common in the binary system. From that one finds that large binary numbers can be added using two simple steps, without excessive carry operations. In the following example, two numerals are being added together: 1 1 1 0 1 1 1 1 1 02 (95810) and 1 0 1 0 1 1 0 0 1 12 (69110), using the traditional carry method on the left, and the long carry method on the right:
Traditional Carry Method Long Carry Method vs. 1 1 1 1 1 1 1 1 (carried digits) 1 ← 1 ← carry the 1 until it is one digit past the "string" below 1 1 1 0 1 1 1 1 1 0The top row shows the carry bits used. Instead of the standard carry from one column to the next, the lowest-ordered "1" with a "1" in the corresponding place value beneath it may be added and a "1" may be carried to one digit past the end of the series. The "used" numbers must be crossed off, since they are already added. Other long strings may likewise be cancelled using the same technique. Then, simply add together any remaining digits normally. Proceeding in this manner gives the final answer of 1 1 0 0 1 1 1 0 0 0 12 (164910). In our simple example using small numbers, the traditional carry method required eight carry operations, yet the long carry method required only two, representing a substantial reduction of effort.1 1 101 1 1 1 10 cross out the "string", + 1 0 1 0 1 1 0 0 1 1 + 1 010 1 1 0 011 and cross out the digit that was added to it ——————————————————————— —————————————————————— = 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1
Addition table
The binary addition table is similar, but not the same, as the truth table of the logical disjunction operation0 1 0 0 1 1 1 10 . The difference is that
, while
.
Subtraction
Further information: signed number representations and two's complementSubtraction works in much the same way:
- 0 − 0 → 0
- 0 − 1 → 1, borrow 1
- 1 − 0 → 1
- 1 − 1 → 0
* * * * (starred columns are borrowed from) 1 1 0 1 1 1 0 − 1 0 1 1 1 ---------------- = 1 0 1 0 1 1 1
* (starred columns are borrowed from) 1 0 1 1 1 1 1 - 1 0 1 0 1 1 ---------------- = 0 1 1 0 1 0 0
Subtracting a positive number is equivalent to adding a negative number of equal absolute value. Computers use signed number representations to handle negative numbers—most commonly the two's complement notation. Such representations eliminate the need for a separate "subtract" operation. Using two's complement notation subtraction can be summarized by the following formula:
A − B = A + not B + 1
Multiplication
Multiplication in binary is similar to its decimal counterpart. Two numbers A and B can be multiplied by partial products: for each digit in B, the product of that digit in A is calculated and written on a new line, shifted leftward so that its rightmost digit lines up with the digit in B that was used. The sum of all these partial products gives the final result.
Since there are only two digits in binary, there are only two possible outcomes of each partial multiplication:
- If the digit in B is 0, the partial product is also 0
- If the digit in B is 1, the partial product is equal to A
1 0 1 1 (A) × 1 0 1 0 (B) --------- 0 0 0 0 ← Corresponds to the rightmost 'zero' in B + 1 0 1 1 ← Corresponds to the next 'one' in B + 0 0 0 0 + 1 0 1 1 --------------- = 1 1 0 1 1 1 0Binary numbers can also be multiplied with bits after a binary point:
1 0 1 . 1 0 1 A (5.625 in decimal) × 1 1 0 . 0 1 B (6.25 in decimal) ------------------- 1 . 0 1 1 0 1 ← Corresponds to a 'one' in B + 0 0 . 0 0 0 0 ← Corresponds to a 'zero' in B + 0 0 0 . 0 0 0 + 1 0 1 1 . 0 1 + 1 0 1 1 0 . 1 --------------------------- = 1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)See also Booth's multiplication algorithm.
Multiplication table
The binary multiplication table is the same as the truth table of the logical conjunction operation0 1 0 0 0 1 0 1 .
Division
-
See also: Division algorithm
In the example below, the divisor is 1012, or 5 decimal, while the dividend is 110112, or 27 decimal. The procedure is the same as that of decimal long division; here, the divisor 1012 goes into the first three digits 1102 of the dividend one time, so a "1" is written on the top line. This result is multiplied by the divisor, and subtracted from the first three digits of the dividend; the next digit (a "1") is included to obtain a new three-digit sequence:
1 ___________ 1 0 1 ) 1 1 0 1 1 − 1 0 1 ----- 0 0 1The procedure is then repeated with the new sequence, continuing until the digits in the dividend have been exhausted:
1 0 1 ___________ 1 0 1 ) 1 1 0 1 1 − 1 0 1 ----- 1 1 1 − 1 0 1 ----- 1 0Thus, the quotient of 110112 divided by 1012 is 1012, as shown on the top line, while the remainder, shown on the bottom line, is 102. In decimal, 27 divided by 5 is 5, with a remainder of 2.
Square root
The process of taking a binary square root digit by digit is the same as for a decimal square root, and is explained here. An example is:
1 0 0 1 --------- √ 1010001 1 --------- 101 01 0 -------- 1001 100 0 -------- 10001 10001 10001 ------- 0Bitwise operations
Main article: bitwise operationThough not directly related to the numerical interpretation of binary symbols, sequences of bits may be manipulated using Boolean logical operators. When a string of binary symbols is manipulated in this way, it is called a bitwise operation; the logical operators AND, OR, and XOR may be performed on corresponding bits in two binary numerals provided as input. The logical NOT operation may be performed on individual bits in a single binary numeral provided as input. Sometimes, such operations may be used as arithmetic short-cuts, and may have other computational benefits as well. For example, an arithmetic shift left of a binary number is the equivalent of multiplication by a (positive, integral) power of 2.
Conversion to and from other numeral systems
Decimal
To convert from a base-10 integer to its base-2 (binary) equivalent, the number is divided by two. The remainder is the least-significant bit. The quotient is again divided by two; its remainder becomes the next least significant bit. This process repeats until a quotient of one is reached. The sequence of remainders (including the final quotient of one) forms the binary value, as each remainder must be either zero or one when dividing by two. For example, (357)10 is expressed as (101100101)2.[28]
Conversion from base-2 to base-10 simply inverts the preceding algorithm. The bits of the binary number are used one by one, starting with the most significant (leftmost) bit. Beginning with the value 0, the prior value is doubled, and the next bit is then added to produce the next value. This can be organized in a multi-column table. For example, to convert 100101011012 to decimal:
-
Prior value × 2 + Next bit Next value 0 × 2 + 1 = 1 1 × 2 + 0 = 2 2 × 2 + 0 = 4 4 × 2 + 1 = 9 9 × 2 + 0 = 18 18 × 2 + 1 = 37 37 × 2 + 0 = 74 74 × 2 + 1 = 149 149 × 2 + 1 = 299 299 × 2 + 0 = 598 598 × 2 + 1 = 1197
The fractional parts of a number are converted with similar methods. They are again based on the equivalence of shifting with doubling or halving.Binary 1 0 0 1 0 1 0 1 1 0 1 Decimal 1×210 + 0×29 + 0×28 + 1×27 + 0×26 + 1×25 + 0×24 + 1×23 + 1×22 + 0×21 + 1×20 = 1197
In a fractional binary number such as 0.110101101012, the first digit is, the second
, etc. So if there is a 1 in the first place after the decimal, then the number is at least
, and vice versa. Double that number is at least 1. This suggests the algorithm: Repeatedly double the number to be converted, record if the result is at least 1, and then throw away the integer part.
For example,10, in binary, is:
-
Converting Result 0. 0.0 0.01 0.010 0.0101
Or for example, 0.110, in binary, is:
-
Converting Result 0.1 0. 0.1 × 2 = 0.2 < 1 0.0 0.2 × 2 = 0.4 < 1 0.00 0.4 × 2 = 0.8 < 1 0.000 0.8 × 2 = 1.6 ≥ 1 0.0001 0.6 × 2 = 1.2 ≥ 1 0.00011 0.2 × 2 = 0.4 < 1 0.000110 0.4 × 2 = 0.8 < 1 0.0001100 0.8 × 2 = 1.6 ≥ 1 0.00011001 0.6 × 2 = 1.2 ≥ 1 0.000110011 0.2 × 2 = 0.4 < 1 0.0001100110
The final conversion is from binary to decimal fractions. The only difficulty arises with repeating fractions, but otherwise the method is to shift the fraction to an integer, convert it as above, and then divide by the appropriate power of two in the decimal base. For example:
in binary) into (
in hexadecimal) and then converting (
in hexadecimal) into (
in decimal).
For very large numbers, these simple methods are inefficient because they perform a large number of multiplications or divisions where one operand is very large. A simple divide-and-conquer algorithm is more effective asymptotically: given a binary number, it is divided by 10k, where k is chosen so that the quotient roughly equals the remainder; then each of these pieces is converted to decimal and the two are concatenated. Given a decimal number, it can be split into two pieces of about the same size, each of which is converted to binary, whereupon the first converted piece is multiplied by 10k and added to the second converted piece, where k is the number of decimal digits in the second, least-significant piece before conversion.
Hexadecimal
Main article: Hexadecimal
Binary may be converted to and from hexadecimal somewhat more easily. This is because the radix of the hexadecimal system (16) is a power of the radix of the binary system (2). More specifically, 16 = 24, so it takes four digits of binary to represent one digit of hexadecimal, as shown in the adjacent table.0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1
To convert a hexadecimal number into its binary equivalent, simply substitute the corresponding binary digits:
- 3A16 = 0011 10102
- E716 = 1110 01112
- 10100102 = 0101 0010 grouped with padding = 5216
- 110111012 = 1101 1101 grouped = DD16
- C0E716 = (12 × 163) + (0 × 162) + (14 × 161) + (7 × 160) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,38310
Octal
Main article: OctalBinary is also easily converted to the octal numeral system, since octal uses a radix of 8, which is a power of two (namely, 23, so it takes exactly three binary digits to represent an octal digit). The correspondence between octal and binary numerals is the same as for the first eight digits of hexadecimal in the table above. Binary 000 is equivalent to the octal digit 0, binary 111 is equivalent to octal 7, and so forth.
-
Octal Binary 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
- 658 = 110 1012
- 178 = 001 1112
- 1011002 = 101 1002 grouped = 548
- 100112 = 010 0112 grouped with padding = 238
- 658 = (6 × 81) + (5 × 80) = (6 × 8) + (5 × 1) = 5310
- 1278 = (1 × 82) + (2 × 81) + (7 × 80) = (1 × 64) + (2 × 8) + (7 × 1) = 8710
Representing real numbers
Non-integers can be represented by using negative powers, which are set off from the other digits by means of a radix point (called a decimal point in the decimal system). For example, the binary number 11.012 thus means:
-
1 × 21 (1 × 2 = 2) plus 1 × 20 (1 × 1 = 1) plus 0 × 2−1 (0 × 1⁄2 = 0) plus 1 × 2−2 (1 × 1⁄4 = 0.25)
All dyadic rational numbershave a terminating binary numeral—the binary representation has a finite number of terms after the radix point. Other rational numbers have binary representation, but instead of terminating, they recur, with a finite sequence of digits repeating indefinitely. For instance
=
= 0.0101010101…2
=
= 0.10110100 10110100 10110100...2
Binary numerals which neither terminate nor recur represent irrational numbers. For instance,
- 0.10100100010000100000100… does have a pattern, but it is not a fixed-length recurring pattern, so the number is irrational
- 1.0110101000001001111001100110011111110… is the binary representation of
, the square root of 2, another irrational. It has no discernible pattern. See irrational number.
See also
- Binary code
- Binary-coded decimal
- Finger binary
- Gray code
- Linear feedback shift register
- Offset binary
- Quibinary
- Reduction of summands
- Redundant binary representation
- Repeating decimal
- SZTAKI Desktop Grid searches for generalized binary number systems up to dimension 11.
- Two's complement
References
- Chrisomalis, Stephen (2010), Numerical Notation: A Comparative History, Cambridge University Press, pp. 42–43, ISBN 9780521878180.
- Rudman, Peter Strom (2007), How Mathematics Happened: The First 50,000 Years, Prometheus Books, pp. 135–136, ISBN 9781615921768.
- "Base System". Retrieved 31 August 2016.
Further reading
- Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC. Boca Raton, FL: CRC Press. p. 37. ISBN 0-8493-7189-9.
- Redmond, Geoffrey; Hon, Tze-Ki (2014). Teaching the I Ching. Oxford University Press. ISBN 0-19-976681-9.
External links
| Wikimedia Commons has media related to Binary numeral system. |
- Binary System at cut-the-knot
- Conversion of Fractions at cut-the-knot
- Binary Digits at Math Is Fun
- How to Convert from Decimal to Binary at wikiHow
- Learning exercise for children at CircuitDesign.info
- Binary Counter with Kids
- "Magic" Card Trick
- Quick reference on Howto read binary
- Binary converter to HEX/DEC/OCT with direct access to bits
- Sir Francis Bacon's BiLiteral Cypher system, predates binary number system.
- Leibniz' binary numeral system, 'De progressione dyadica', 1679, online and analyzed on BibNum [click 'à télécharger' for English analysis]
Navigation menu
Interaction
Tools
Print/export
In other projects
Languages
- Afrikaans
- العربية
- Azərbaycanca
- تۆرکجه
- বাংলা
- Bân-lâm-gú
- Беларуская
- Български
- Boarisch
- Bosanski
- Brezhoneg
- Català
- Чӑвашла
- Čeština
- ChiShona
- Dansk
- Deutsch
- Eesti
- Ελληνικά
- Español
- Esperanto
- Euskara
- فارسی
- Français
- Furlan
- Gaeilge
- Galego
- 한국어
- Հայերեն
- हिन्दी
- Hrvatski
- Bahasa Indonesia
- Interlingua
- Íslenska
- Italiano
- עברית
- Basa Jawa
- ಕನ್ನಡ
- ქართული
- Қазақша
- Kreyòl ayisyen
- Latina
- Latviešu
- Lietuvių
- Lumbaart
- Magyar
- Македонски
- മലയാളം
- मराठी
- Bahasa Melayu
- Mirandés
- Монгол
- Nederlands
- नेपाली
- 日本語
- Norsk bokmål
- Norsk nynorsk
- Олык марий
- ਪੰਜਾਬੀ
- Polski
- Português
- Română
- Русский
- Scots
- Sesotho sa Leboa
- Shqip
- සිංහල
- Simple English
- سنڌي
- Slovenčina
- Slovenščina
- Soomaaliga
- Српски / srpski
- Srpskohrvatski / српскохрватски
- Basa Sunda
- Suomi
- Svenska
- ไทย
- Türkçe
- Українська
- اردو
- Tiếng Việt
- 文言
- West-Vlams
- ייִדיש
- 粵語
- 中文
- This page was last edited on 6 June 2017, at 22:45.






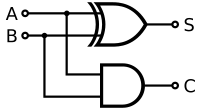






No comments:
Post a Comment