In
quantum computing, a qubit (/ ˈ k juː b ɪ t /) or quantum bit
(sometimes qbit) is a unit of quantum information—the quantum analogue
of the classical bit.
Qubit
From Wikipedia, the free encyclopedia
 |
Unsolved problem in physics:
|
In
quantum computing, a
qubit (
) or
quantum bit (sometimes
qbit) is a unit of
quantum information—the quantum analogue of the classical
bit. A qubit is a
two-state quantum-mechanical system, such as the
polarization of a single
photon:
here the two states are vertical polarization and horizontal
polarization. In a classical system, a bit would have to be in one
state or the other. However quantum mechanics allows the qubit to be in a
superposition of both states at the same time,
[citation needed] a property which is fundamental to quantum computing.
[citation needed]
Origin of the concept and name
The concept of the qubit was unknowingly introduced by
Stephen Wiesner in 1983, in his proposal for
quantum money, which he had tried to publish for over a decade.
[1][2]
The coining of the term "qubit" is attributed to
Benjamin Schumacher.
[3] In the acknowledgments of his paper, Schumacher states that the term
qubit was invented in jest due to its phonological resemblance with an ancient unit of length called
cubit, during a conversation with
William Wootters.
The paper describes a way of compressing states emitted by a quantum
source of information so that they require fewer physical resources to
store. This procedure is now known as
Schumacher compression.
Bit versus qubit
The
bit
is the basic unit of information. It is used to represent information by
computers. Regardless of its physical realization, a bit has two
possible states typically thought of as 0 and 1, but more generally—and
according to applications—interpretable as true and false, or any other
dichotomous choice. An analogy to this is a light switch—its off
position can be thought of as 0 and its on position as 1.
A qubit has a few similarities to a classical bit, but is overall
very different. There are two possible outcomes for the measurement of a
qubit—usually 0 and 1, like a bit. The difference is that whereas the
state of a bit is either 0 or 1, the state of a qubit can also be a
superposition of both.
[4]
It is possible to fully encode one bit in one qubit. However, a qubit
can hold even more information, e.g. up to two bits using
superdense coding.
Representation
The two states in which a qubit may be measured are known as
basis states (or basis
vectors). As is the tradition with any sort of
quantum states, they are represented by
Dirac—or
"bra–ket"—notation. This means that the two computational basis states are conventionally written as

and

(pronounced "ket 0" and "ket 1").
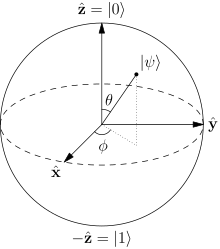
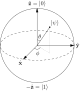
Qubit states
Bloch sphere representation of a qubit. The probability amplitudes in the text are given by

and
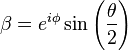
.
A pure qubit state is a linear
superposition of the basis states. This means that the qubit can be represented as a
linear combination of

and

:
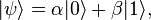
where
α and
β are
probability amplitudes and can in general both be
complex numbers.
When we measure this qubit in the standard basis, the probability of outcome

is
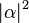
and the probability of outcome

is

. Because the absolute squares of the amplitudes equate to probabilities, it follows that
α and
β must be constrained by the equation
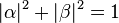
simply because this ensures you must measure either one state or the
other (the total probability of all possible outcomes must be 1).
Bloch sphere
The possible states for a single qubit can be visualised using a
Bloch sphere
(see diagram). Represented on such a sphere, a classical bit could only
be at the "North Pole" or the "South Pole", in the locations where

and

are respectively. The rest of the surface of the sphere is inaccessible
to a classical bit, but a pure qubit state can be represented by any
point on the surface. For example, the pure qubit state

would lie on the equator of the sphere, on the positive y axis.
The surface of the sphere is two-dimensional space, which represents the
state space of the pure qubit states. This state space has two local
degrees of freedom. It might at first sight seem that there should be four degrees of freedom, as α and β are
complex numbers with two degrees of freedom each. However, one degree of freedom is removed by the constraint
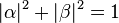
. Another, the overall
phase
of the state, has no physically observable consequences, so we can
arbitrarily choose α to be real, leaving just two degrees of freedom.
It is possible to put the qubit in a
mixed state,
a statistical combination of different pure states. Mixed states can be
represented by points inside the Bloch sphere. A mixed qubit state has
three degrees of freedom: the angles

and

, as well as the length r of the vector that represents the mixed state.
Operations on pure qubit states
There are various kinds of physical operations that can be performed on pure qubit states.
[citation needed]
- A quantum logic gate can operate on a qubit: mathematically speaking, the qubit undergoes a unitary transformation. Unitary transformations correspond to rotations of the qubit vector in the Bloch sphere.
- Standard basis measurement is an operation in which information is gained about the state of the qubit. The result of the measurement will be either
 , with probability
, with probability 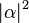 , or
, or  , with probability
, with probability  . Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is
. Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is  , α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
, α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
Entanglement
An important distinguishing feature between a qubit and a classical bit is that multiple qubits can exhibit
quantum entanglement. Entanglement is a
nonlocal
property that allows a set of qubits to express higher correlation than
is possible in classical systems. Take, for example, two entangled
qubits in the
Bell state
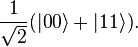
In this state, called an
equal superposition, there are equal probabilities of measuring either
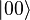
or
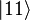
, as

.
Imagine that these two entangled qubits are separated, with one each
given to Alice and Bob. Alice makes a measurement of her qubit,
obtaining—with equal probabilities—either

or

. Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a

, Bob must measure the same, as
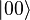
is the only state where Alice's qubit is a

. Entanglement also allows multiple states (such as the
Bell state
mentioned above) to be acted on simultaneously, unlike classical bits
that can only have one value at a time. Entanglement is a necessary
ingredient of any quantum computation that cannot be done efficiently on
a classical computer. Many of the successes of quantum computation and
communication, such as
quantum teleportation and
superdense coding, make use of entanglement, suggesting that entanglement is a
resource that is unique to quantum computation.
Quantum register
A number of qubits taken together is a
qubit register.
Quantum computers perform calculations by manipulating qubits within a register. A
qubyte (quantum byte) is a collection of eight qubits.
[5]
Variations of the qubit
Similar to the qubit, a
qutrit is a unit of quantum information in a 3-level quantum system. This is analogous to the unit of classical information
trit. The term "
qudit" is used to denote a unit of quantum information in a
d-level quantum system.
Physical representation
Any two-level system can be used as a qubit. Multilevel systems can
be used as well, if they possess two states that can be effectively
decoupled from the rest (e.g., ground state and first excited state of a
nonlinear oscillator). There are various proposals. Several physical
implementations which approximate two-level systems to various degrees
were successfully realized. Similarly to a classical bit where the state
of a transistor in a processor, the magnetization of a surface in a
hard disk and the presence of current in a cable can all be used to
represent bits in the same computer, an eventual quantum computer is
likely to use various combinations of qubits in its design.
The following is an incomplete list of physical implementations of qubits, and the choices of basis are by convention only.
Qubit storage
In a paper entitled: "Solid-state quantum memory using the
31P nuclear spin", published in the October 23, 2008 issue of the journal
Nature,
[6]
a team of scientists from the U.K. and U.S. reported the first
relatively long (1.75 seconds) and coherent transfer of a superposition
state in an electron spin "processing" qubit to a
nuclear spin
"memory" qubit. This event can be considered the first relatively
consistent quantum data storage, a vital step towards the development of
quantum computing.
Recently, a modification of similar systems (using charged rather than
neutral donors) has dramatically extended this time, to 3 hours at very
low temperatures and 39 minutes at room temperature.
[7]
See also
References

 and
and  (pronounced "ket 0" and "ket 1").
(pronounced "ket 0" and "ket 1"). and
and  :
: is
is 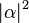 and the probability of outcome
and the probability of outcome  is
is  . Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation
. Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation and
and  are respectively. The rest of the surface of the sphere is inaccessible
to a classical bit, but a pure qubit state can be represented by any
point on the surface. For example, the pure qubit state
are respectively. The rest of the surface of the sphere is inaccessible
to a classical bit, but a pure qubit state can be represented by any
point on the surface. For example, the pure qubit state  would lie on the equator of the sphere, on the positive y axis.
would lie on the equator of the sphere, on the positive y axis.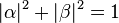 . Another, the overall phase
of the state, has no physically observable consequences, so we can
arbitrarily choose α to be real, leaving just two degrees of freedom.
. Another, the overall phase
of the state, has no physically observable consequences, so we can
arbitrarily choose α to be real, leaving just two degrees of freedom. and
and  , as well as the length r of the vector that represents the mixed state.
, as well as the length r of the vector that represents the mixed state. , with probability
, with probability 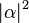 , or
, or  , with probability
, with probability  . Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is
. Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is  , α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
, α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.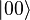 or
or 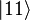 , as
, as  .
. or
or  . Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a
. Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a  , Bob must measure the same, as
, Bob must measure the same, as 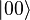 is the only state where Alice's qubit is a
is the only state where Alice's qubit is a  . Entanglement also allows multiple states (such as the Bell state
mentioned above) to be acted on simultaneously, unlike classical bits
that can only have one value at a time. Entanglement is a necessary
ingredient of any quantum computation that cannot be done efficiently on
a classical computer. Many of the successes of quantum computation and
communication, such as quantum teleportation and superdense coding, make use of entanglement, suggesting that entanglement is a resource that is unique to quantum computation.
. Entanglement also allows multiple states (such as the Bell state
mentioned above) to be acted on simultaneously, unlike classical bits
that can only have one value at a time. Entanglement is a necessary
ingredient of any quantum computation that cannot be done efficiently on
a classical computer. Many of the successes of quantum computation and
communication, such as quantum teleportation and superdense coding, make use of entanglement, suggesting that entanglement is a resource that is unique to quantum computation.

 and
and 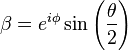 .
.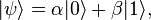
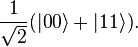
No comments:
Post a Comment